This year I decided to contribute to the F# Advent Calendar, a yearly event where members of the F# community share their thoughts with others through a series of blog posts and articles.

In light of the holiday season I chose a project that is related to something many of us our doing this time of year - wrapping gifts! But let me stop you before you get carried away with visions of present-wrapping robots or machine learning algorithms for selecting the best gifts. It’s not going to be quite that exciting, but it could help you be a more efficient wrapper.

I’m going to be walking through the implementation of one of my favorite algorithms: the Gift Wrapping algorithm. It’s an algorithm that is used to compute the “convex hull” of a set of points, which is the smallest subset of points which form a convex polygon that encapsulates all the remaining points.

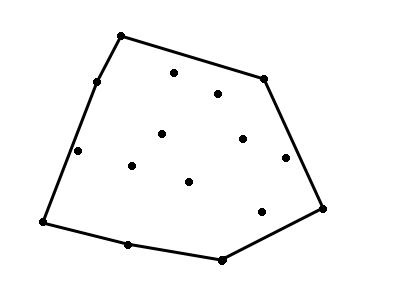
The Gift Wrapping algorithm (also known as Jarvis march) is an interesting solution to the problem as it operates by wrapping the points similar to how you would wrap a gift. It has a time complexity of O(nh) where n is the total number of points and h is the number of points in the hull, so its performance is dependent on the size of the result set. It’s often outperformed by other convex hull algorithms, but it is simple to implement and interesting nonetheless. You can learn about some of the other algorithms here.

The Algorithm

We will be be working off of the pseudocode that is presented on the wikipedia page:

algorithm jarvis(S) is
    // S is the set of points
    // P will be the set of points which form the convex hull. Final set size is i.
    pointOnHull = leftmost point in S // which is guaranteed to be part of the CH(S)
    i := 0
    repeat
        P[i] := pointOnHull
        endpoint := S[0]      // initial endpoint for a candidate edge on the hull
        for j from 0 to |S| do
            // endpoint == pointOnHull is a rare case and can happen only when j == 1 and a better endpoint has not yet been set for the loop
            if (endpoint == pointOnHull) or (S[j] is on left of line from P[i] to endpoint) then
                endpoint := S[j]   // found greater left turn, update endpoint
        i := i + 1
        pointOnHull = endpoint
    until endpoint = P[0]      // wrapped around to first hull point

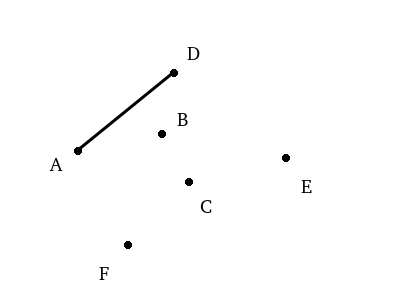
The algorithm is best explained visually. We start with a point that we know will be on the hull, the leftmost point in the set, which is point A in this case.

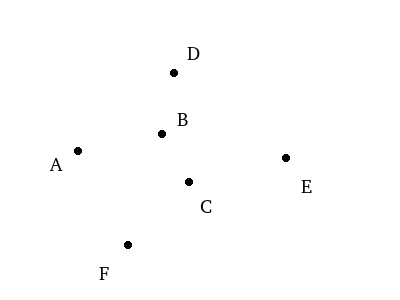
We then choose an arbitrary point in the set as our first endpoint. Let’s say we chose B. From here, we’re going to imagine a line through A and B by which we’re going to judge other points.

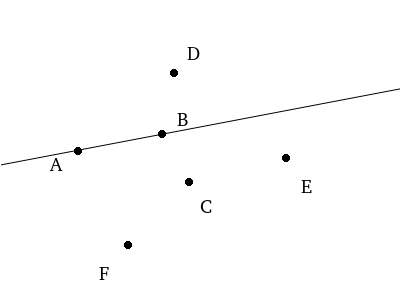
For each other point in the set we need to determine whether it is left of the line or right of the line. If it is left of the line, it becomes the new endpoint by which we test the remaining points. By the time we test every point, we’ll have identified the leftmost point (rotationally, relative to the last hull point) which must be on the hull as well.

So for example, we have A which is our pointOnHull, B which is our current endpoint, and we’re going to begin testing points. We might start with C. The point falls to the right of the line through A and B so we know C cannot be on the hull.

If we tested D next, we’d see that D is in fact to the left of the line. Since it’s further left than B, it becomes our new endpoint.

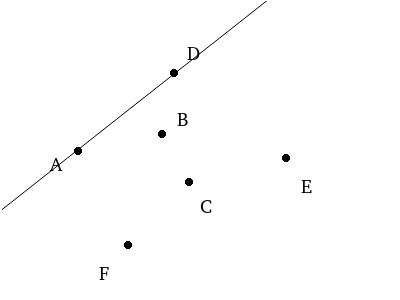
We would continue on to test E and F, both of which would be right of the line through A and D, and determine that D is the next point on the hull.

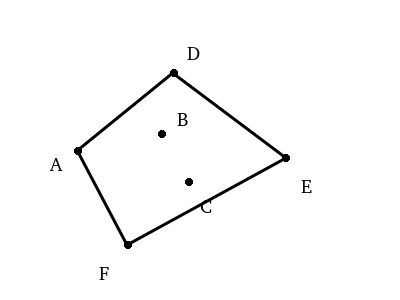
This process repeats with D as our new pointOnHull, then the next one we find, and so on until we make our way back to the original starting point. By then we’ll have finished identifying our convex hull.

An Imperative Approach

Before we implement the algorithm in F# functionally, I’d like to begin by showing it in the imperative style mirroring the pseudocode above. This will let us get to a working implementation quickly and give us a good starting point for an iterative refactor.

The only custom type we need for this is a simple Point record:

type Point = {
    X: int;
    Y: int;
}

The imperative implementation of our function toConvexHull: Point list -> Point list is the following:

let toConvexHull (points: Point list): Point list = 
    // Start at the leftmost point since it is guaranteed to be on the hull
    let startingPoint = points |> List.minBy (fun p -> p.X)

    let mutable hull = []
    let mutable pointOnHull = startingPoint

    let mutable atStartingPoint = false
    while not atStartingPoint do
        hull <- pointOnHull::hull
        let mutable endpoint = points |> List.head
        for candidatePoint in points do
            if (endpoint = pointOnHull) || (candidatePoint |> isLeftOfLine (pointOnHull, endpoint)) then
                endpoint <- candidatePoint
        pointOnHull <- endpoint
        atStartingPoint <- startingPoint = endpoint
    hull

You should be able to line it up with the pseudocode pretty easily. We get our startingPoint by finding the point in our list with the smallest X coordinate and then initialize our list of hull points and our first pointOnHull. From there we enter our while loop where we add our current pointOnHull to the hull and choose an arbitrary endpoint (the first item in the list) to test with. We then test each point in the set, and if it is further left than our endpoint, we make it the new endpoint. Once we’re done, we set pointOnHull to endpoint since it is our newest hull point. Then as long as that point wasn’t the one we started with, we start all over to find the next hull point.

The one bit that we’ve skimmed over on purpose is the isLeftOfLine function. That is the predicate we use to determine if candidatePoint is left of the line created by pointOnHull and endpoint. In order to explain its implementation, we’ll need to take a detour into some math…

One way we can determine whether a point is to the left (or right) of a line is by using a cross product. Cross products are used for all sorts of things that I don’t remember from school, but the one that is useful for us is the fact that the sign of the cross product determines whether the angle created by two vectors is clockwise or counter-clockwise. For example, imagine we have two vectors V1 and V2.

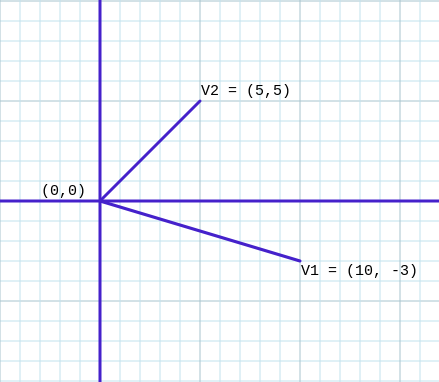
The cross product, V1 X V2, will be positive since the angle from V1 to V2 is counter-clockwise. The opposite cross product, V2 X V1, is negative because the angle is clockwise. I don’t know why this is true, just that it is.

So now if we have a line from A to B and a third point P, we can use the cross product to determine if the angle between A->B and A->P is counter-clockwise, which would mean that P is left of the line.

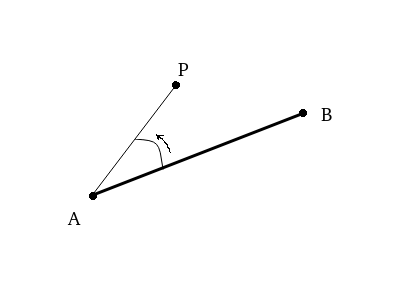
To do that we treat B and P as the two vectors, but since they’re starting from A rather than the origin (0,0) we need to subtract the vector A from each of them.

The formula to calculate the cross product of B and P is:

B X P = (Bx * Py) - (By * Px)

Which becomes the following after we subtract the vector A from both B and P:

(B - A) X (P - A) = ((Bx - Ax) * (Py - Ay)) - ((By - Ay) * (Px - Ax))

We can translate this into code as the function directionFromLine which is then used by isLeftOfLine.

type Direction =
    | Left
    | Right
    | Colinear

let directionFromLine a b p =
    let crossProduct =
        (b.X - a.X) * (p.Y - a.Y) - (b.Y - a.Y) * (p.X - a.X)
    if crossProduct > 0 then Left
    elif crossProduct < 0 then Right
    else Colinear

let isLeftOfLine (line: Point * Point) point =
    let (lineStart, lineEnd) = line
    match (directionFromLine lineStart lineEnd point) with
    | Left -> true
    | _ -> false

With that we’ve got a complete implementation of the Gift Wrapping algorithm, but it’s littered with loops and mutable state. Next we’ll work towards refactoring that code to be more functional in nature.

Towards a Functional Solution

Let’s approach this by trying to convert a piece at a time. The meat of the function is in the two loops: an inner for loop that is used to identify the next hull point and a surrounding while loop that collects them all.

We should be able to extract that inner for loop pretty easily. It takes a point it knows is on the hull, a point that could be on the hull, and then tests each of the other points, replacing the assumed new hull point whenever it finds one that is further left. This could be rewritten as a single reduce.

let findNextPointOnHull pointOnHull candidatePoints =
    candidatePoints
    |> List.reduce (fun endpoint candidatePoint ->
        if (endpoint = pointOnHull) || (candidatePoint |> isLeftOfLine (pointOnHull, endpoint)) then
            candidatePoint
        else
            endpoint)

The function passed to List.reduce takes an accumulator and the next element in the list. It starts by passing the first two elements of the list in, then the result of that with the third element, the result of that with the fourth element, and so on. We utilize this behavior by passing the potential hull point, endpoint as the accumulated value. In the function we test whether the next point in the list, candidatePoint is left of endpoint, and if so pass that point as the accumulated value instead. This lets us mimic the behavior of the for loop without the need for mutable state.

let toConvexHull (points: Point list): Point list = 
    let findNextPointOnHull pointOnHull candidatePoints =
        candidatePoints
        |> List.reduce (fun endpoint candidatePoint ->
            if (endpoint = pointOnHull) || (candidatePoint |> isLeftOfLine (pointOnHull, endpoint)) then
                candidatePoint
            else
                endpoint)

    let startingPoint = points |> List.minBy (fun p -> p.X)

    let mutable hull = []
    let mutable pointOnHull = startingPoint

    let mutable atStartingPoint = false
    while not atStartingPoint do
        hull <- pointOnHull:: hull
        pointOnHull <- findNextPointOnHull pointOnHull points
        atStartingPoint <- startingPoint = pointOnHull
    hull

Our code is looking a little more functional, but there’s still some work to do. A few mutable values remain and it would be great if we could eliminate that while loop.

Functional Gift Wrapping

The easiest way for us to replace that while loop is through recursion. This part of the algorithm is a natural fit since we are using a known hull point to find the next hull point, then using that new hull point to find the next hull point, and on and on, until we eventually hit our stop condition by running into our initial starting point. From there we just need to collect all of the values we’ve identified.

let rec findPointsOnHull startingPoint pointOnHull candidatePoints =
    let nextPointOnHull = findNextPointOnHull pointOnHull points
    if nextPointOnHull = startingPoint then
        [nextPointOnHull]
    else
        nextPointOnHull::(findPointsOnHull startingPoint nextPointOnHull candidatePoints)

With that recursive helper function defined, our final toConvexHull function looks like the following:

let toConvexHull (points: Point list): Point list = 
    let findNextPointOnHull pointOnHull candidatePoints =
        candidatePoints
        |> List.reduce (fun endpoint candidatePoint ->
            if (endpoint = pointOnHull) || (candidatePoint |> isLeftOfLine (pointOnHull, endpoint)) then
                candidatePoint
            else
                endpoint)

    let rec findPointsOnHull startingPoint pointOnHull candidatePoints =
        let nextPointOnHull = findNextPointOnHull pointOnHull points
        if nextPointOnHull = startingPoint then
            [nextPointOnHull]
        else
            nextPointOnHull::(findPointsOnHull startingPoint nextPointOnHull candidatePoints)

    let startingPoint = points |> List.minBy (fun p -> p.X)
    let pointOnHull = startingPoint
    findPointsOnHull startingPoint pointOnHull points

Conclusion

We now have a working, functional implementation of the Gift Wrapping algorithm.

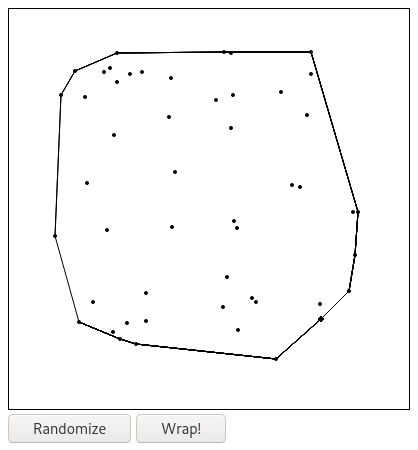
If you would like to play with the application or view the complete source code, you can find the repository here. I implemented the small Fable application you see above. It will let you randomize the points and generate the convex hull. The three implementations of the algorithm can be found in src/GiftWrapping.fs.

Happy holidays!